– “A Comparison about Graph-based Approaches for Extractive Text Summarization”
How we bump into this (the story)
We are facing a text summarization task when building content for career pages (e.g. FAQ or overview for a job title). In this post, we will take FAQ as an example. We want to come up with top K representative question and answer pairs from a forum-like dataset (can be from various sources: for example, ACME QnA is one) where we have tons of questions pre-defined or asked by users, and for each question, we have numerous answers with different quality. Do note that the content that goes into production will need additional moderation process (done by human) after the machine generates the summarized dataset.
Text summarization techniques overview
There are in general two types of approaches for text summarization
- Extraction-based: pick keywords or representative sentences and combine them to make a summary.
- Abstraction-based: create new phrases and sentences that relay the most useful information from the original text.
The abstractive algorithms are relatively new, as the development is only accelerated recently with the advance of deep learning algorithms. Some models have achieved satisfactory results on specific datasets. But they are often difficult to develop and also depend on the quality of the labelled datasets to achieve good results.
Here, we focus on extractive methods first, as it is likely to generate results quickly with less uncertainty in the sense that it picks existing sentences instead of trying to craft one. And our problem actually resonates with the multi-document summarization problem where each answer itself can be treated as a document.
How we find out TextRank, LexRank and DivRank
One popular method to do extractive text summarization is TextRank. It borrows the idea from PageRank and constructs the transition matrix using a text-based similarity scoring function between every pair of sentences.
While using this model, we realized that when ask TextRank to identify the most K representative sentence, it often output sentences that are quite similar with each other. This is fine as long as we only want to have one sentence as the summary of a document. However, what we are facing is actually a multi-document problem, and when summarizing multiple documents, there is a greater risk of selecting duplicate or highly redundant sentences to place in the same summary. We want to pick top K sentences from N documents, with those top K sentences to be representative as well as diverse at the same time. To solve this issue, we then proposed a reranking step after TextRank and implemented it with Python code. What’s more, the number of upvotes for each answer is also incorporated as the prior distribution such that the answer with higher upvote count will be favored in case of random jump.
Later, with more extensive search online, I found that the approach proposed by us actually has been proposed by others already. Specifically, in the LexRank paper and the MEAD framework it has adopted, the reranking steps were included. And personalized page rank uses the prior distribution for the nodes in the random jump part. Moreover, other algorithms like DivRank provide different updating formula during the PageRank iteration process to promote diversity. Hence, it seems a perfect time for us to run a comparison of those algorithms and combine the best points for our use.
What they have in common
- A graph is constructed by creating a vertex(node) for each sentence in the corpus.
The edges between sentences are based on some form of similarity score (e.g. semantic similarity or content overlap). The specific similarity function may be different. - After the graph is constructed, the sentences are ranked by applying PageRank (or modified PageRank) to the resulting graph. A summary is formed by combining the top ranking sentences.
Just as a reminder, PageRank works like this:
The PageRank algorithm tries to find out the central nodes in the graph by using the concept of random walk with teleporting. The score of a node depends on the score of its neighbors. From a vertex $s$, the walk either ’teleports’ to a random vertex in the graph
with probability $1-d$, or with probability $d$ (damping factor) jumps into one of the neighbors of $s$
$$p(s) = (1-d)\frac{1}{N} + d\sum_{v \in V}\frac{sim(s, v)}{\sum_{z\in V} sim(z, v)}p(v)$$
The Personalized PageRank algorithm goes one step ahead and uses the prior distribution for the nodes in the ranking process. Hence, nodes with a high prior value will be favored in case of random jump.
$$p(s) = (1-d)\frac{p^{-} (s)}{\sum_{z\in V} p^{-} (s)} + d\sum_{v \in V}\frac{sim(s, v)}{\sum_{z\in V} sim(z, v)}p(v)$$
where $p^{-}$ is the prior distribution. For example, in our case, we can use normalized upvotes count as a prior distribution.
What’s different
Similarity measures
- TextRank: the number of words two sentences have in common normalized by the sentences’ lengths
$$Similarity(S_i, S_j) = \frac{|{w_k|w_k \in S_i \& w_k \in S_j}|}{log(|S_i|)+log(|S_j|)}å$$ LexRank: cosine similarity of TF-IDF vectors:
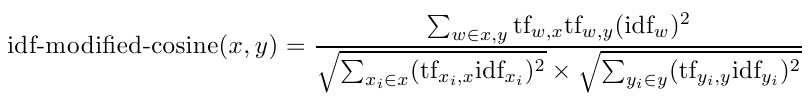
They use the bag-of-words model to represent each sentence as an N-dimensional vector, where N is the number of all possible words in the target language. They use this score to build the similarity matrix (normalized per row to have row-sum = 1).There is an additional filtering step on the similarity matrix proposed by LexRank - “Since we are interested in significant similarities, we can eliminate some low values in this matrix by defining a threshold”
DivRank: they use the same as LexRank to construct the initial transition matrix. But the transition matrix will not remain the same during the iteration process (whereas in TextRank and LexRank, the transition matrix will not change)
Note: in both TextRank and DivRank papers, they both mention that other similarity measures can be used and they may give different performance depending on the task and dataset on hand.
Single document vs. Multi-document
TextRank and LexRank (without post-processing steps) are mainly used for single document (or similar topics) summarization.
To address the redundancy issue in multi-document summarization, LexRank applies a heuristic post-processing (reranking) step that builds up a summary by adding sentences in rank order, but discards any sentences that are too similar to ones already placed in the summary. The method used is called Cross-Sentence Information Subsumption (CSIS).
DivRank however, designs for multi-document summarization by nature, as it considers both ‘centrality’ and ‘diversity’ simultaneously in the ranking process.
Modified PageRank in DivRank
DivRank is motivated from a general time-variant random walk process known as the vertex-reinforced random walk in mathematics literature. It uses the following formula in the updating process: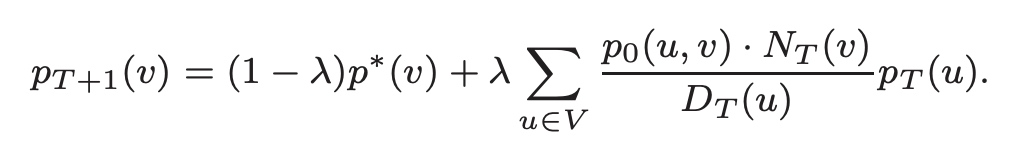
where $D_T(u) = \sum_{v\in V}p_0(u, v) p_T(u)$ and $p_T(u, v)$ is the transition probability from any state $u$ to any state $v$ at time $T$. $p_0(u, v)$ is the “organic” transition probability prior to any reinforcement, which can be estimated as in a regular time-homogenous random walk.
Other notes
LexRank was actually used as part of a larger summarization system called MEAD.
Many ideas/steps in MEAD are quite useful and can be borrowed to improve the summarization pipeline
- Reranking with Cross-Sentence Information Subsumption (CSIS) or Maximal Marginal Relevance (MRR)
- Combined the ranking score with other features like sentence position and length using a linear combination with either user-specified or automatically tuned weights
Diversity Approaches
From the above, we actually have seen two methods of promoting diversity. And in fact, they demonstrates the two categories that the current popular methods for diversity fall into:
- Greedy selection methods: Iteratively selects one vertex at a time such that the next vertex is central, and as diverse as possible from the set of ranked (picked) vertices - the reranking technique used by MEAD is one example
- Unified ranking methods: Both ‘centrality’ and ‘diversity’ are considered simultaneously in the ranking process, which runs only once - DivRank is one example
References: